回帰分析は、データ科学や統計学において広く使用される重要な手法です。この手法は、変数間の関係性を理解し、将来の値を予測するのに役立ちます。本記事では、回帰分析の概要から具体的な手法、そして将来の展望までを探ります。データの世界における重要性を考える上で、回帰分析の役割を理解することは不可欠です。
はじめに: 回帰分析の概要
回帰分析とは何か?
回帰分析は、変数間の関係性を調査し、ある変数が別の変数にどのように影響を与えるかを理解するための統計手法です。主に予測や解釈に使用されます。
回帰分析の重要性と応用範囲
回帰分析は、さまざまな分野で広く応用されています。経済学やマーケティング、医学や社会科学など、多くの領域でデータの分析や予測に活用されています。また、ビジネスにおいても市場動向の分析や顧客の行動予測など、意思決定の支援に不可欠な手法となっています。
単回帰分析の解説
単回帰分析とは?
単回帰分析は、1つの説明変数が1つの目的変数にどのように影響するかを調査する統計手法です。独立変数と従属変数の間の直線的な関係をモデル化し、その関係性を評価します。
単回帰分析の基本概念
単回帰分析では、独立変数(説明変数)と従属変数(目的変数)の関係を表す直線を求めます。この直線は、最小二乗法を用いてモデル化され、データに最もよく適合する直線が求められます。
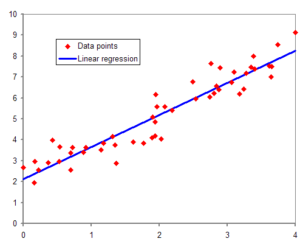
単回帰分析の手法と計算方法
単回帰分析の手法には、変数間の相関係数や回帰係数の計算が含まれます。また、最小二乗法を用いて回帰直線を求める手法も重要です。
以下に計算式を記載しますが、仕事上計算をされる方以外はあまり詳しく理解する必要はありません。
- データの収集: まず、説明変数(独立変数)と目的変数(従属変数)のデータを収集します。これらのデータは通常、実際の観測値や実験結果から得られます。
- 回帰直線の式の決定: 次に、回帰直線の式を決定します。単回帰分析では、次の式を用いて回帰直線を求めます。
y = b0 + b1x
ここで、yは目的変数、xは説明変数、b0は切片、b1は回帰係数です。 - 最小二乗法によるパラメータの推定: 最小二乗法を用いて、観測値と回帰直線との残差の二乗和を最小化するパラメータ
b0とb1を求めます。これは、観測値と回帰直線の距離を最小化することで、モデルの精度を向上させる手法です。 - 回帰係数の推定: 最小二乗法により、回帰係数
b0とb1を推定します。具体的な計算方法は、b1 = (n(∑xy) - (∑x)(∑y)) / (n(∑x2) - (∑x)2)
ここで、nはサンプルサイズ、∑xyはxとyの積の合計、∑xはxの合計、∑yはyの合計、∑x2はxの二乗の合計です。 - 切片の推定: 切片
b0は次の式で計算されます。b0 = (∑y - b1(∑x)) / n - 回帰直線の式の完成: 求めた回帰係数
b0とb1を元に、回帰直線の式を完成させます。
単回帰分析の例題と解釈方法
単回帰分析の例題では、例えば広告費用が売上に与える影響を調査するケースなどが挙げられます。また、回帰直線の傾きや切片を解釈することで、変数間の関係性を理解することができます。
重回帰分析の解説
重回帰分析とは?
重回帰分析は、複数の説明変数が目的変数に与える影響を同時に評価する統計手法です。単回帰分析が1つの説明変数と目的変数の関係を分析するのに対して、重回帰分析では複数の説明変数を考慮します。これにより、複数の要因が目的変数にどのように影響するかをより包括的に分析することが可能です。
重回帰分析の基本原理
重回帰分析の基本原理は、複数の説明変数を組み合わせて目的変数の変動を説明する回帰方程式を推定することです。通常、最小二乗法が使用され、回帰係数の推定値が求められます。また、重回帰分析では説明変数間の相互作用も考慮されることがあります。
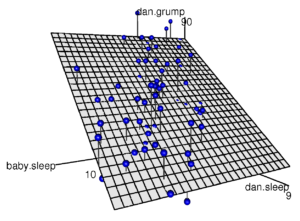
重回帰分析の実践的な手法
重回帰分析の実践的な手法には、変数の選択方法やモデルの適合度評価、多重共線性の検討などが含まれます。変数の選択には、統計的手法や専門知識に基づく方法があります。モデルの適合度評価には、決定係数やAICなどの指標を用います。また、多重共線性の検討では、相関行列やVIF(分散拡大係数)を確認します。
重回帰分析の計算方法
重回帰分析は、複数の説明変数が目的変数に与える影響を分析する方法です。以下では、重回帰分析の計算方法について説明します。
以下に具体的な計算方法を記載しますが、仕事上で計算を使用しない場合は読み飛ばしてください。
1. 重回帰方程式の式の決定
重回帰方程式は、以下のように表されます。
Y = β0 + β1X1 + β2X2 + … + βnXn
ここで、Yは目的変数、X1, X2, …, Xnは説明変数、β0, β1, β2, …, βnは回帰係数です。
2. 最小二乗法によるパラメータの推定
最小二乗法を用いて、観測値と回帰直線との残差の二乗和を最小化するパラメータ β0, β1, β2, …, βnを求めます。
3. 回帰係数の推定
最小二乗法により、回帰係数 β0, β1, β2, …, βnを推定します。
4. 切片の推定
切片 β0は、最小二乗法を用いて次のように計算されます。
β0 = ∑Y – β1(∑X1) – β2(∑X2) – … – βn(∑Xn)
5. 回帰方程式の完成
求めた回帰係数 β0, β1, β2, …, βnを元に、回帰方程式を完成させます。
以上が、重回帰分析の計算方法になります。
重回帰分析の適用事例と解析手法
重回帰分析はさまざまな分野で利用されています。例えば、マーケティングでの売上予測や経済学での価格決定要因の分析などがあります。解析手法としては、変数選択手法や多重共線性の検討、回帰診断統計量の確認などがあります。また、重回帰分析の結果を解釈する際には、各説明変数の係数や相互作用の影響を理解し、ビジネス上の意義を明確にする必要があります。
単回帰と重回帰: 比較と適用
単回帰と重回帰は、回帰分析の手法でありながら、いくつかの重要な違いや共通点があります。
単回帰と重回帰の違いと共通点
違い:
- 説明変数の数: 単回帰では1つの説明変数を用いて目的変数を予測しますが、重回帰では複数の説明変数を用いて目的変数を予測します。
- モデルの複雑さ: 単回帰は比較的単純なモデルであり、説明変数と目的変数の関係を直線的に表現します。一方、重回帰はより複雑なモデルであり、説明変数と目的変数の関係を複数の変数を考慮して表現します。
- 解釈の難易度: 重回帰の場合、複数の説明変数が相互作用する可能性があるため、モデルの解釈がより難しくなります。一方、単回帰では説明変数と目的変数の関係が直線的であるため、解釈が比較的容易です。
共通点:
- 回帰係数の推定: 単回帰も重回帰も、最小二乗法を用いて回帰係数を推定します。つまり、観測値とモデルの予測値の誤差を最小化するように回帰係数を求めます。
- 残差の評価: どちらの場合も、残差の分布やパターンを評価して、モデルの適合度を確認します。残差がランダムに分布していることが理想的です。
単回帰と重回帰の選択基準と活用法
単回帰と重回帰のどちらを選択するかは、データの性質や分析の目的によって異なります。以下では、それぞれの選択基準と活用法について詳しく説明します。
単回帰の選択基準と活用法:
- データの単純性: 説明変数と目的変数の関係が直線的であり、他の説明変数との相互作用が少ない場合に適しています。例えば、気温とアイスクリームの売上など、単一の要因が影響を与える場合に有効です。
- モデルの解釈性: モデルの解釈が比較的容易であり、説明変数と目的変数の関係を直線的に表現することができます。そのため、初心者や非専門家にも理解しやすく、説得力のある結果を得ることができます。
- データの規模: サンプルサイズが比較的小さい場合や、計算リソースが限られている場合に適しています。単回帰は計算コストが低く、シンプルなモデルなので、小規模なデータセットでも効果的に利用することができます。
重回帰の選択基準と活用法:
- 複数の要因の影響を考慮: 複数の説明変数が目的変数に影響を与える場合や、相互作用が存在する場合に適しています。例えば、家の価格を予測する場合、広さや立地条件、築年数など複数の要因が価格に影響を与えるため、重回帰が適しています。
- モデルの柔軟性: 複数の説明変数を組み合わせることで、モデルの柔軟性が向上します。これにより、現実の複雑なデータに対応し、より正確な予測や解析を行うことができます。
- データの規模と計算リソース: サンプルサイズが大きく、複雑なデータ構造を持つ場合には、重回帰を適用することが一般的です。ただし、計算コストやモデルの解釈の複雑さに注意する必要があります。
5. 結論: 回帰分析の重要性と展望
5-1. 回帰分析の価値と今後の発展
回帰分析は、データ分析や予測モデリングにおいて非常に重要な手法です。以下に、その価値と今後の発展について考察します。
回帰分析の価値:
- 現実世界の現象の理解: 回帰分析は、複数の変数間の関係性を明らかにすることができます。これにより、現象や事象の背後にあるメカニズムやパターンを理解するのに役立ちます。
- 予測と意思決定の支援: 回帰モデルを構築することで、将来の値を予測し、意思決定をサポートすることが可能です。例えば、ビジネスや経済分野での需要予測や価格設定の最適化などに活用されています。
- 因果関係の推定: 回帰分析は因果関係を推定するための手法としても利用されます。相関関係があるかどうかを調べるだけでなく、一つの変数が他の変数に与える影響を理解することができます。
- モデルの検証と改善: 回帰分析はモデルの検証や改善にも役立ちます。実際のデータとモデルの予測値を比較することで、モデルの正確性や有用性を評価し、必要に応じて改良を加えることができます。
今後の発展:
回帰分析は、データサイエンスやビジネス分野でますます重要性を増しています。今後の発展として、以下のようなトレンドが考えられます。
- 高度なモデルの開発: 機械学習や深層学習の進展により、より複雑で高度な回帰モデルが開発されると予想されます。これにより、より正確な予測や因果関係の推定が可能になるでしょう。
- リアルタイム分析の増加: ビッグデータ技術の発展により、リアルタイムで大規模なデータセットを分析することが可能になります。これにより、リアルタイムでの予測や意思決定が可能になり、ビジネスプロセスの最適化が進むでしょう。
- 非線形回帰の探求: 現実世界のデータはしばしば非線形の関係性を持つことがあります。今後は、非線形回帰モデルの探求や開発が進み、より現実的なモデリングが可能になるでしょう。
5-2. 回帰分析の応用がもたらすメリットと将来展望
回帰分析の応用は、さまざまな分野で多岐に渡ります。以下では、そのメリットと将来の展望について考察します。
回帰分析のメリット:
- 予測精度の向上: 回帰分析は、データからの傾向やパターンを明らかにし、将来の値を予測するのに役立ちます。これにより、ビジネス戦略や政策決定の基盤となる情報を提供することができます。
- 因果関係の理解: 回帰分析は、変数間の因果関係を推定するための有力な手法です。これにより、特定の要因が結果に与える影響を理解し、効果的な介入や改善策を見出すことができます。
- 効率的なリソース利用: ビジネスや組織において、回帰分析はリソースの効率的な利用に貢献します。効果的な予測やリスク管理により、生産性や収益性の向上が期待されます。
将来展望:
回帰分析の将来展望は、データ駆動型の意思決定や産業のデジタル化の進展に密接に関連しています。以下に、将来の展望を示します。
- データ駆動型組織の普及: ビジネスや組織において、データ駆動型の意思決定がますます重要となります。回帰分析はその基盤となる手法の一つであり、今後もますます普及していくでしょう。
- AIとの統合: 人工知能(AI)や機械学習の技術との統合が進むことで、より高度な予測モデルや意思決定支援システムが開発されると予想されます。これにより、回帰分析の応用範囲がさらに拡大するでしょう。
- 個人化と精度の向上: ビッグデータやクラウドテクノロジーの進展により、個人レベルでの予測や分析が可能になります。これにより、サービスや製品の個別化が進み、顧客満足度や効果的なマーケティングが実現されるでしょう。
番外編:回帰分析私見
以下、簡単に理解するための内容を記載しておきます。
回帰分析:ある変数と他の1つまたは複数の変数の関係を見る分析
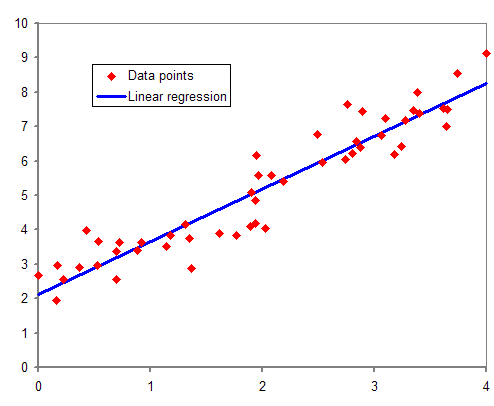
・ある変数と1つの変数との関係を見る
→単回帰分析
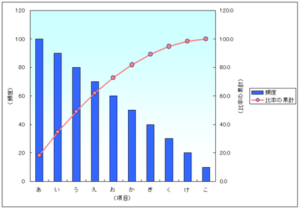
・ある変数と複数の変数との関係を見る
→重回帰分析


















コメント